Rasterization: a Practical Implementation The Rasterization Stage

camera space에 물체를 raster space로 projection 한 이후, 이번에 해결할 문제는 아래와 같다.

- triangle과 겹치는 픽셀을 찾아야 함.

- 겹치는 픽셀에 어떤 색을 세팅할 지 결정해야 함.

 

위 두 가지의 문제를 해결하기 위해 우리는 아래의 방법을 이용한다.

- edge function

- barycentric cordinates

 

Edge Function

triangle과 겹치는 픽셀을 찾는 많은 알고리즘이 있다. edge function은 그 중 하나이다.

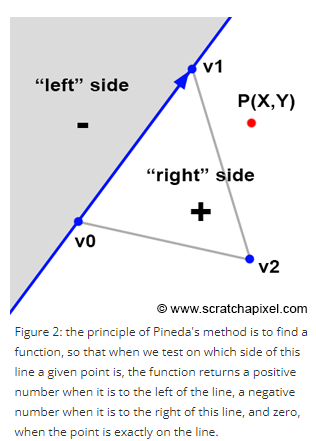
삼각형의 한 변을 연장하면 2d space를 2개로 나눌 수 있다. edge function은 2개로 나눈 space중 왼쪽 좌표값을 넣으면 음수값을 반환하고, 오른쪽 좌표값을 넣으면 양수 값을 반환, 선 위에 있으면 0을 반환하는 함수를 말한다.

 

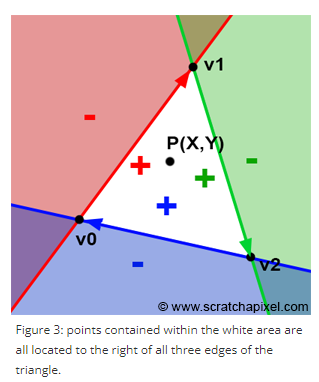
좌표상의 한 점을 edge function으로 모든 변에 대해 수행했을 때, 모든 값이 양수 이면 이 점은 삼각형 안에 있는 점이다.

 

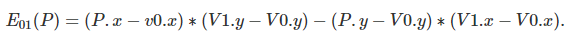
edge function은 위와 같다.

이는 vector(v1 - v0)와 vector(P - v0) cross product 값과 같다.

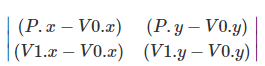
A = (P - V0), B = (V1 - V0) 로 치환하면

 

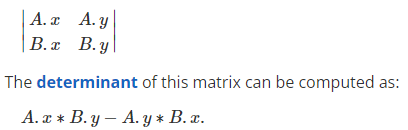
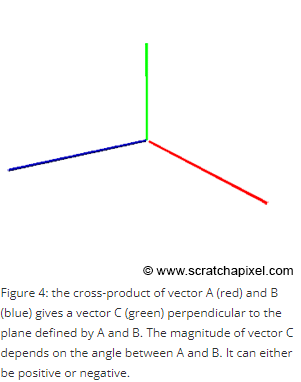
Red와 Blue vector를 cross product하면 Green vector를 구할 수 있다. Red와 Blue가 똑같은 방향을 바라보거나 반대방향을 바라보면 Green의 magnitude는 0이다.

 

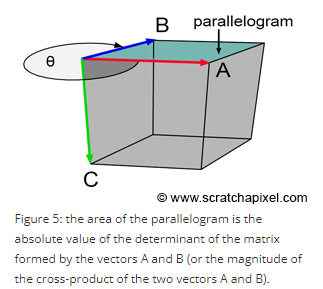
다른 방식으로 해석할 수도 있다. 3차원 좌표공간에서 vector A와 vector B로 만들어진 사다리꼴의 넓이는 vector A, vector B cross product의 magnitude이다.

 

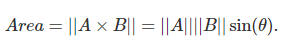
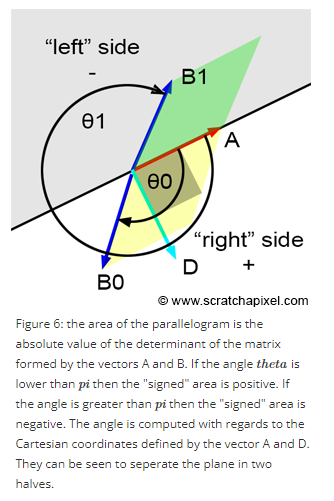
vector B가 vector A와 이와 직교하는 vector D로 만든 좌표공간의 오른쪽에 있으면 양수, 반대 쪽에 있으면 음수값이 나온다.

 

 

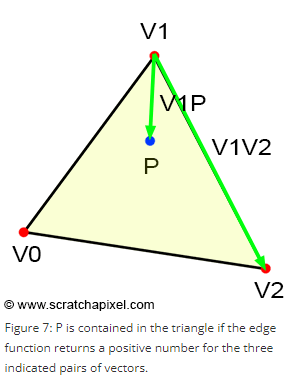
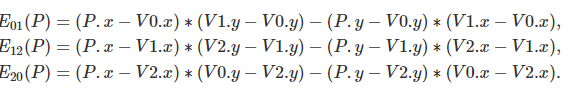
세 변에 대해서 테스트하여 점 P가 삼각형 내부에 있는지 확인할 수 있다.

pseudo code로 보면,

bool edgeFunction(const Vec2f &a, const Vec3f &b, const Vec2f &c) 
{ 
    return ((c.x - a.x) * (b.y - a.y) - (c.y - a.y) * (b.x - a.x) >= 0); 
} 
 
bool inside = true; 
inside &= edgeFunction(V0, V1, p); 
inside &= edgeFunction(V1, V2, p); 
inside &= edgeFunction(V2, V0, p); 
 
if (inside == true) { 
    // point p is inside triangles defined by vertices v0, v1, v2
    ... 
}

삼각형 vertices를 시계방향으로 정의하는가 반시계방향으로 정의하는가에 따라 edge function 기대값이 달라진다.

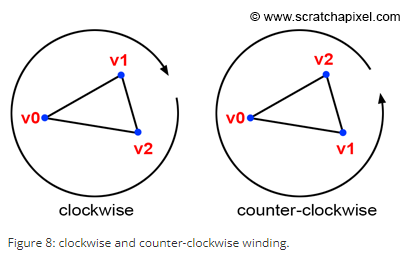
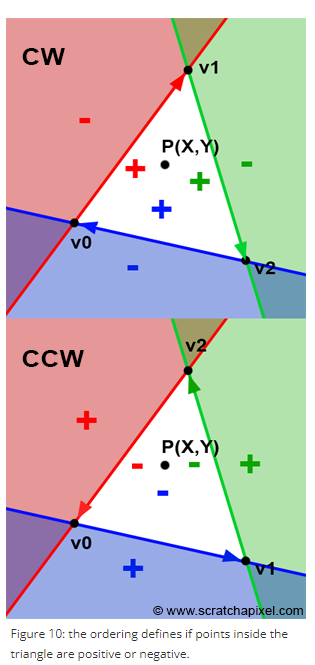
점P가 삼각형 내부에 있으면,

시계 방향일 경우

  - edge function은 양수를 리턴한다.

반시계 방향일 경우

  - 음수를 리턴한다.

 

Barycentric Coordinates

barycentric coordinates는 삼각형 내부의 점 P를 아래와 같이 표현하는 방법을 말한다.

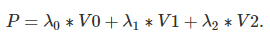
람다0 ~ 람다 2는 floating point이다.

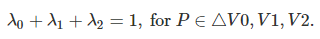
각 람다의 범위는 [0,1]이고 세 람다를 모두 합하면 1이다. vertices의 interpolation 형태이기 때문에 람다를 각 vertices의 가중치라고 볼 수도 있다.

 

CG에서는 삼각형 vertices와 관련있는 property를 vertex attribute라고 한다. 흔히 사용하는 vertex attribute는 colors, normals, texture coordinates가 있다. 이러한 property의 interpolate가 필요할 때 barycentric coordinates를 사용한다.

 

barycentric coordinates를 구하는 방법을 알아보자.

삼각형 내부의 점 P로 삼각형을 내부 삼각형 3개로 나눌 수 있다. 내부 삼각형 넓이와 전체 삼각형 넓이의 비로 람다를 구할 수 있다.

 

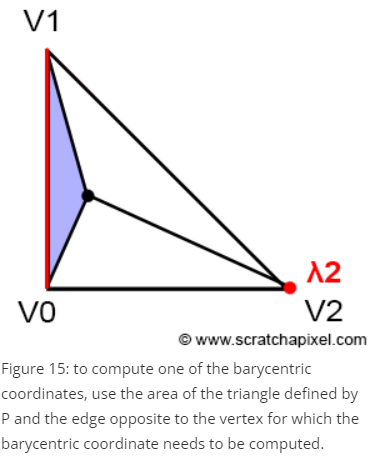
예를 들어 람다 2는 삼각형 V0V1P 넓이와 관련있다. 삼각형 V0V1P 넓이를 전체 삼각형의 넓이로 나누면 람다 2를 구할 수 있다.

삼각형 V0V1P넓이는 edge function(VO, V1, P) * 1/2와 같다.

 

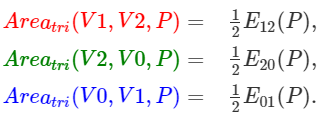
모든 람다를 넓이의 비로 표현하면,

이를 pseudo code로 나타내면 다음과 같다.

 

float edgeFunction(const Vec2f &a, const Vec3f &b, const Vec2f &c) 
{ 
    return (c.x - a.x) * (b.y - a.y) - (c.y - a.y) * (b.x - a.x); 
} 
 
float area = edgeFunction(v0, v1, v2); // area of the triangle multiplied by 2 
float w0 = edgeFunction(v1, v2, p); // signed area of the triangle v1v2p multiplied by 2 
float w1 = edgeFunction(v2, v0, p); // signed area of the triangle v2v0p multiplied by 2 
float w2 = edgeFunction(v0, v1, p); // signed area of the triangle v0v1p multiplied by 2 
 
// if point p is inside triangles defined by vertices v0, v1, v2
if (w0 >= 0 && w1 >= 0 && w2 >= 0) { 
    // barycentric coordinates are the areas of the sub-triangles divided by the area of the main triangle
    w0 /= area; 
    w1 /= area; 
    w2 /= area; 
}

barycentric coordinates는 삼각형 내부의 점P의 위치와 무관하게 구할 수 있다. 삼각형 내부에 P가 있다면 interpolation이라고 하고 바깥에 있으면 extrapolation이라고 한다. extrapolation은 겹치지 않는 점 P에 대해 계산할 필요가 있을 때 사용하며, texture coordinates 계산에 많이 사용한다.

 

Rasterization Rules

삼각형 끝 모서리가 서로 닿으면 해당 픽셀을 두 개의 삼각형이 공유한다. 만약 삼각형이 불투명하다면 이 닿은 부분에 검은 색이 나타나게 된다.

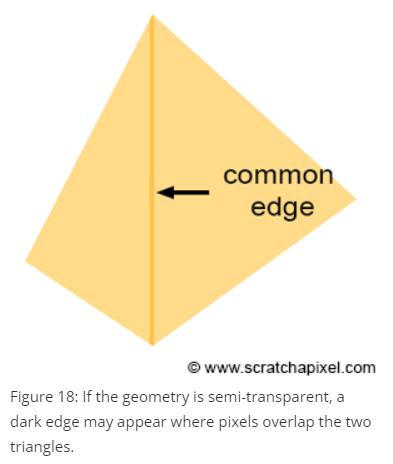
이 문제는 같은 픽셀을 서로 다른 삼각형이 공유하지 못하게 막아서 해결한다. convention 중 top-left rule이라는 것을 소개한다.

삼각형 edge에 픽셀이 있을 때 이 점은 top 또는 left edge의 삼각형에 속한다는 rule이다.

top edge는 수평선이면서 vector V[(X+1)%3] - V[X] 값이 y는 0이고 x는 양수이다.

left edge는 위로 올라가는 edge이다. vector V[(X+1)%3] - V[X] 값이 y는 양수이다.

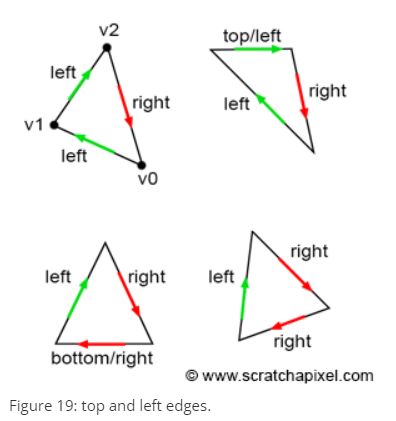
pseudo code로 표현하면 다음과 같다.

// Does it pass the top-left rule?
Vec2f v0 = { ... }; 
Vec2f v1 = { ... }; 
Vec2f v2 = { ... }; 
 
float w0 = edgeFunction(v1, v2, p); 
float w1 = edgeFunction(v2, v0, p); 
float w2 = edgeFunction(v0, v1, p); 
 
Vec2f edge0 = v2 - v1; 
Vec2f edge1 = v0 - v2; 
Vec2f edge2 = v1 - v0; 
 
bool overlaps = true; 
 
// If the point is on the edge, test if it is a top or left edge, 
// otherwise test if  the edge function is positive
overlaps &= (w0 == 0 ? ((edge0.y == 0 && edge0.x > 0) ||  edge0.y > 0) : (w0 > 0)); 
overlaps &= (w1 == 0 ? ((edge1.y == 0 && edge1.x > 0) ||  edge1.y > 0) : (w1 > 0)); 
overlaps &= (w2 == 0 ? ((edge2.y == 0 && edge2.x > 0) ||  edge2.y > 0) : (w2 > 0)); 
 
if (overlaps) { 
    // pixel overlap the triangle
    ... 
}

지금까지 알아본 내용을 합쳐서 프로그램을 짜보자.

 

삼각형을 rasterspace에 project 하는 작업은 미리 해놓았다고 가정한다. 이제 삼각형에 색을 입힌다. 이미지의 모든 픽셀을 순회하면서 edge function을 이용하여 해당 픽셀이 삼각형 내부에 있는지 확인한다. 3개 edge에 대해서 모든 edge function이 양수를 return 하면 픽셀이 삼각형 내부에 있는 것이다. 그 다음 이를 이용해 barycentric coordinates을 계산하고 interpolating 하여 color를 shading한다. 이를 frame buffer에 그리고 이를 ppm 파일에 쓴다.

 

#include <cstdio>
#include <cstdlib>
#include <fstream>

typedef float Vec2[2];
typedef float Vec3[3];
typedef unsigned char Rgb[3];

inline float edgeFunction(const Vec2& a, const Vec2& b, const Vec2& c)
{
    return (c[0] - a[0]) * (b[1] - a[1]) - (c[1] - a[1]) * (b[0] - a[0]);
}

int main(int argc, char** argv)
{
    Vec2 v0 = { 491.407f, 411.407f };
    Vec2 v1 = { 148.593f, 68.5928f };
    Vec2 v2 = { 148.593f, 411.407f };
    Vec3 c0 = { 1, 0, 0 };
    Vec3 c1 = { 0, 1, 0 };
    Vec3 c2 = { 0, 0, 1 };

    const uint32_t w = 512;
    const uint32_t h = 512;

    Rgb* framebuffer = new Rgb[w * h];
    memset(framebuffer, 0x0, w * h * 3);

    float area = edgeFunction(v0, v1, v2);

    for (int32_t j = 0; j < h; ++j)
    {
        for (uint32_t i = 0; i < w; ++i)
        {
            Vec2 p = { i + 0.5f, j + 0.5f };
            float w0 = edgeFunction(v1, v2, p);
            float w1 = edgeFunction(v2, v0, p);
            float w2 = edgeFunction(v0, v1, p);
            if (w0 >= 0 && w1 >= 0 && w2 >= 0)
            {
                w0 /= area;
                w1 /= area;
                w2 /= area;
                float r = w0 * c0[0] + w1 * c1[0] + w2 * c2[0];
                float g = w0 * c0[1] + w1 * c1[1] + w2 * c2[1];
                float b = w0 * c0[2] + w1 * c1[2] + w2 * c2[2];
                framebuffer[j * w + i][0] = (uint8_t)(r * 255);
                framebuffer[j * w + i][1] = (uint8_t)(g * 255);
                framebuffer[j * w + i][2] = (uint8_t)(b * 255);
            }
        }
    }

    std::ofstream ofs;
    ofs.open("./raster2d.ppm");
    ofs << "P6\n" << w << " " << h << "\n255\n";
    ofs.write((char*)framebuffer, w * h * 3);
    ofs.close();

    delete[] framebuffer;
    return 0;
}

 

이렇게 해서 얻은 이미지. 뭔가 잘못된 것 같다..

참조 : Rasterization: a Practical Implementation (The Rasterization Stage) (scratchapixel.com)