Rasterization: a Practical Implementation Improving the Rasterization Algorithm

Rasterization을 최적화하는 몇 가지 기술을 소개한다.

Aliasing and Anti-Aliasing

삼각형을 확대해보면 모서리에 계단 모양의 패턴이 나타난다. 이를 jaggies라고 한다. rasterization하면서 연속적인 공간을 불연속적인 공간(픽셀)로 바꾸면서 나타난 결과이다.

픽셀당 1개의 sample을 render하는 대신, 여러개의 sub pixel로 쪼개 coverage test를 하는 방법으로 이러한 문제를 해결할 수 있다.

 

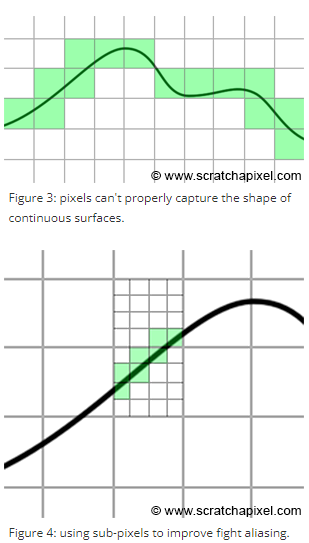
sub pixel로 쪼개놓은 pixel의 최종 color는 sub pixel color를 그 숫자로 나눈 값이 된다.

예를 들어 삼각형이 하얀색이고 4개의 sample 중 2개만 삼각형에 overlap한다면 최종 color는 (0+0+1+1)/4=0.5이다.

 

Rendering Blocks of Pixels

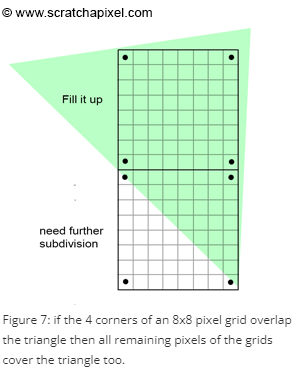
Rasterization을 더 빠르게 하기 위한 technique이다.

block 안 모든 pixel을 testing하는 대신 block의 코너만 먼저 testing한다. 네 모퉁이의 pixel이 모두 하나의 삼각형을 cover하면 나머지 픽셀 역시 삼각형을 cover하기 때문에 연산 횟수를 줄일 수 있다. 만약 interpolation이 필요하면 네 모퉁이의 값을 이용하여 interpolation하면 된다.

 

Optimizing the Edge Function

int orient2d(const Point2D& a, const Point2D& b, const Point2D& c)
{
    return (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);
}

a, b는 삼각형 vertices이고 c는 pixel coordinate이다. bounding box안에서 a와 b는 고정이고 c만 변한다.

먼저 w0를 구한다.

w0 = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);

c.x는 pixel이동 s에 따라 점차 증가한다. 그래서 새로운 w0는 아래와 같이 계산할 수 있다

w0_new = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x+s-a.x);

첫 번째 equation과 두 번째 equation을 빼면

w0_new - w0 = -(b.y-a.y)*s;

이다. 여기서 -(b.y-a.y)*s는 상수이다. s도 1pixel로 매번 같다. 이 연산을 다른 변수 w0step에 저장하여 연산 횟수를 줄일 수 있다.

w0_new = w0 + w0step;

같은 연산을 w1, w2에 대해서 그리고 c.y step에 대해서 할 수 있다.

 

Fixed Point Coordinates

NDC space에서 ratster space로 변환할 때 vertex coordinate은 float 에서 int로 바뀐다.

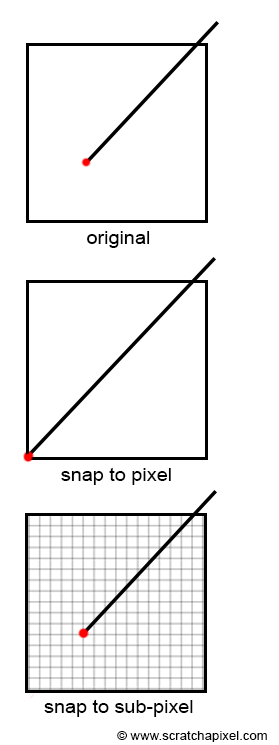
이 때 float 은 가장 가까운 int로 반올림한다. 즉, 원래 좌표와 다르게 가장 가까운 corner 좌표로 snap하는 것이다.

이를 해결하는 방법은 sub-pixel을 인코딩할 수 있는 공간을 미리 만들어 두는 것이다.

GPU는 보통 4bits를 sub-pixel precision을 위해 남겨둔다. 32bit integer 중 1bit는 음,양수를 표시하고 27bits는 vertex coordinate을 위해 쓴다. 그리고 4bits는 sub-pixel 공간에서 snap하기 위해 둔다. 4bits로 16개의 숫자를 표현 할 수 있으므로 16x16의 grid로 sub-pixel을 만들어 좀 더 원래 위치와 가까운 값으로 근사하는 것이다.

 

참조 : Rasterization: a Practical Implementation (Rasterization: a Practical Implementation) (scratchapixel.com)