고정 헤더 영역
상세 컨텐츠
본문
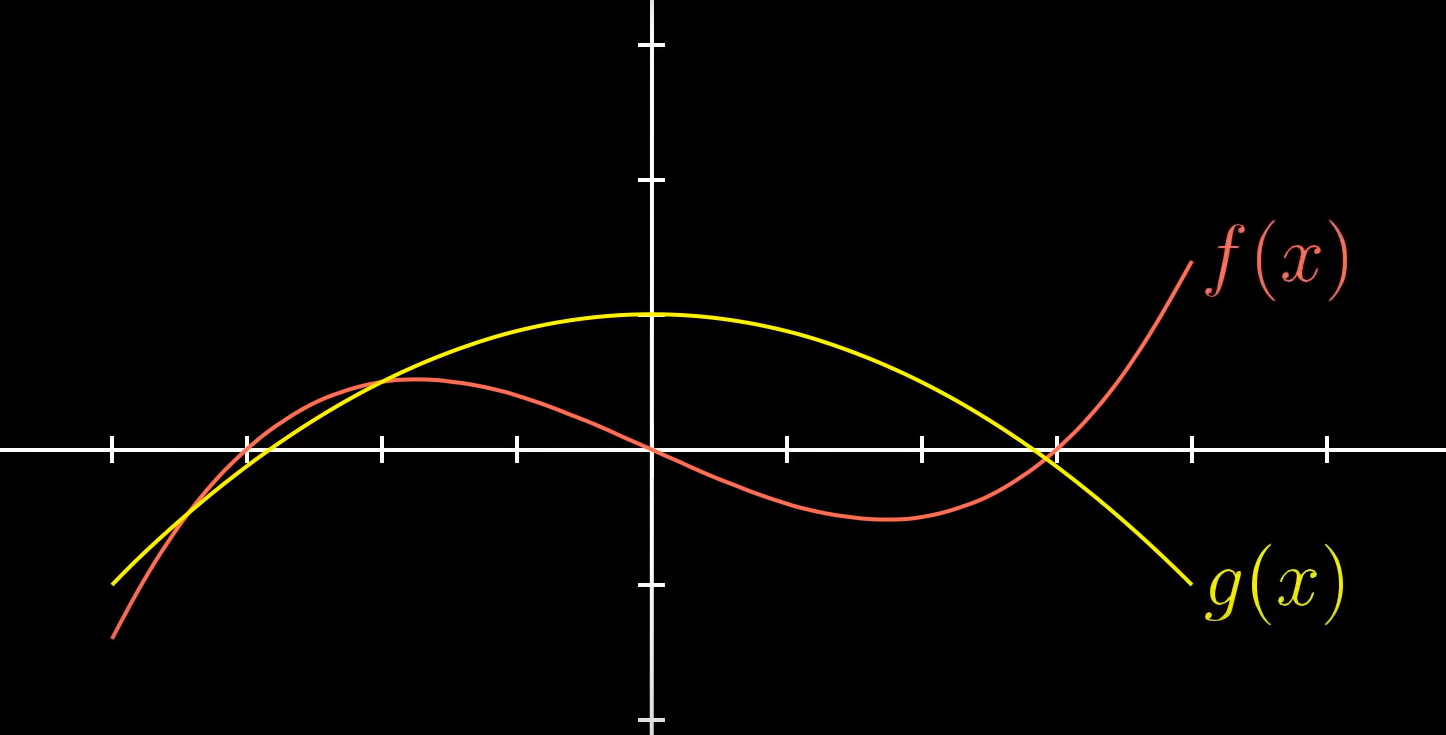
함수는 다른 타입의 벡터로 볼 수 있다.

함수의 합이 위의 성질을 갖고 있고,
스케일링이 아래의 성질을 갖는다면 말이다.
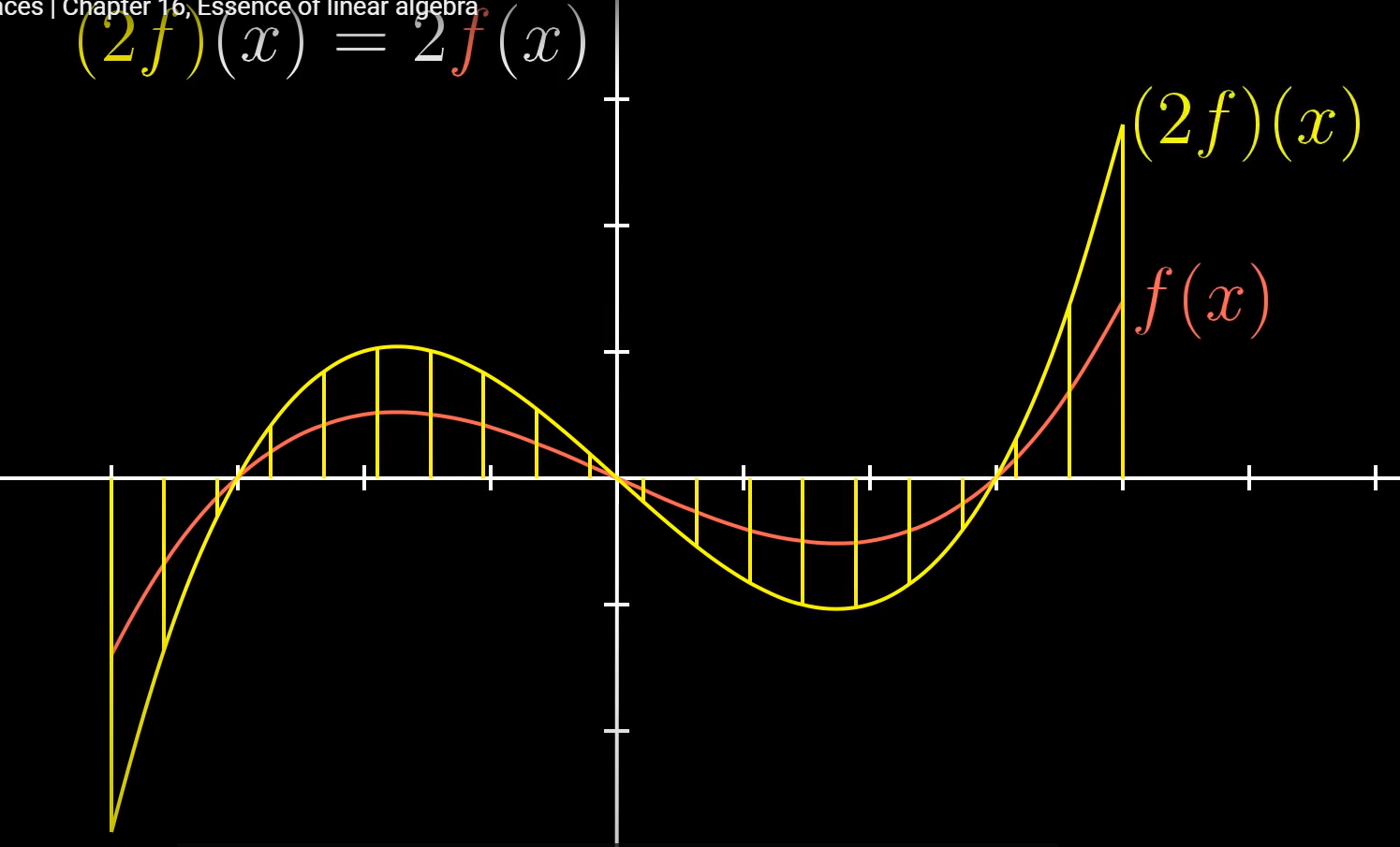
이러한 함수는 지금까지 살펴본 선형대수의 기술을 적용할 수 있다.
기술은 Linear transformation, Null space, Dot products, Eigen-everything 같은 것들이 있다.
함수에 적용하는 선형변환 예를 들어보자면,
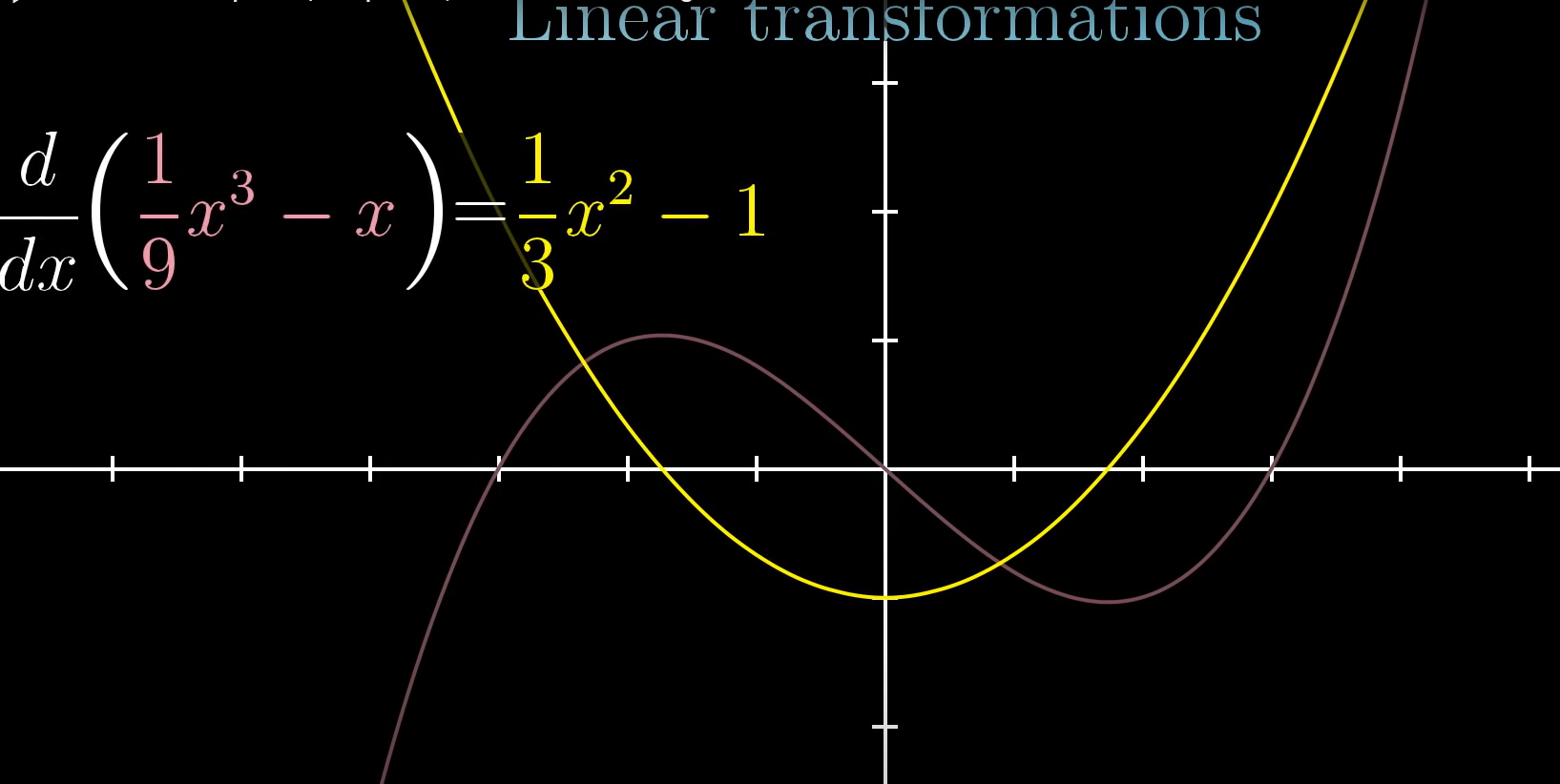
위와 같은 미분함수가 있다.
어떠한 변환이 선형변환이려면 다음과 같은 특징을 갖춰야 한다.
Additivity
Scaling

이를 선형변환은 addition과 scaler multiplication을 보존한다라고 표현한다.
2D 공간에서 이를 표현하면 선형변환이 Grid line을 평행하고 같은 너비만큼 떨어져 있는다.
벡터와 같은 것들 예를 들면, 화살표, 숫자 리스트, 함수들을 벡터 공간이라고 부른다.

이 벡터 공간은 다음 8가지 axiom을 만족해야 한다. (그래야 벡터 공간이라고 부른다.)

이 정의는 addition과 scaling을 만족하기 위한 것이다.
참조 : (4) Abstract vector spaces | Chapter 16, Essence of linear algebra - YouTube
'똑똑한 개발 > 수학' 카테고리의 다른 글
| Trigonometry fundamentals (0) | 2022.06.02 |
|---|---|
| A quick trick for computing eigenvalues (0) | 2022.05.26 |
| Eigenvectors and eigenvalues (0) | 2022.05.22 |
| Change of basis (0) | 2022.05.14 |
| 크래머 공식을 기하학적으로 이해해 보자 (0) | 2022.05.11 |





댓글 영역