고정 헤더 영역
상세 컨텐츠
본문
Eigenvectors, eigenvalues에 대해 알아보자.
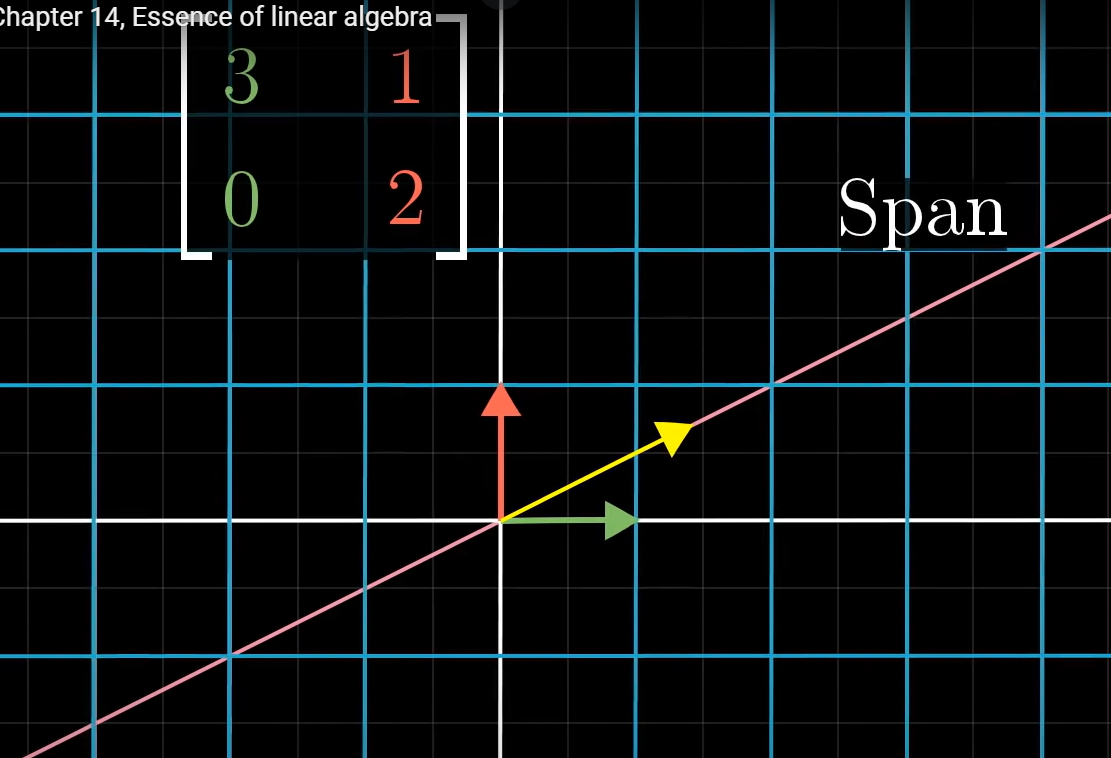
위 그림처럼, 임의의 벡터와 벡터를 지나는 span이 있다.
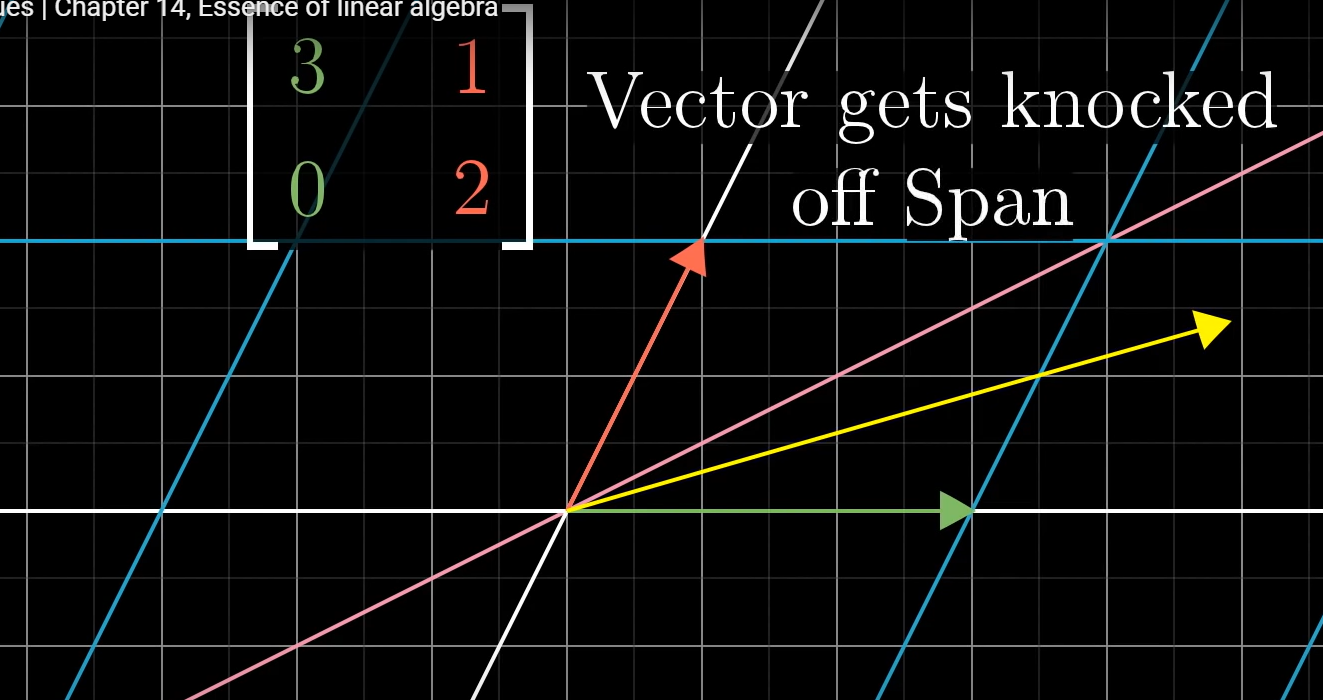
왼쪽 위 상단에 보이는 matrix만큼 선형변환하면 span과 그 위에 있던 벡터는 서로 떨어진다.
그러나 어떤 벡터는 span과 떨어지지 않는데 이를 eigenvectors라고 하고 eigenvectors가 얼만큼 scale 되었는지를 eigenvalue라고 한다.


3차원 공간에서 eigenvector는 eigenvalue가 1이면 rotate axis이다. 줄거나 늘어나지 않고 선형변환을 가해도 변하지 않는 벡터를 중심으로 선형변환이 이루어지는 것은 rotation이기 때문이다.
Eigenvector와 value는 다음의 식으로 나타낼 수 있다.

matrix-vector 곱이 vector를 어떤 상수만큼 scaling 한 것과 같다는 의미다.
오른쪽 식을 왼쪽처럼 matrix-vector곱으로 나타내면, 다음과 같다.

각 basis vector를 람다만큼 스케일링하기 때문이다.
대각성분이 모두 1인 I matrix로 바꿔 아래와 같이 다시 쓸 수 있다.

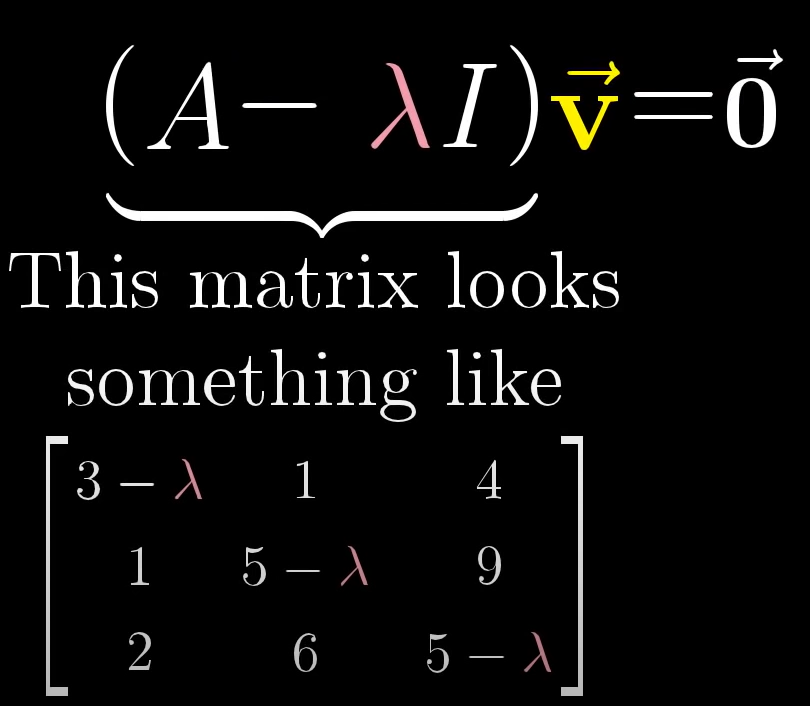
어떤 matrix와 영벡터가 아닌 벡터 곱이 영 벡터가 되려면 matrix의 det가 0이어야 한다. 이는 matrix로 표현한 선형변환이 차원을 축소 시킨다는 말과 같다.
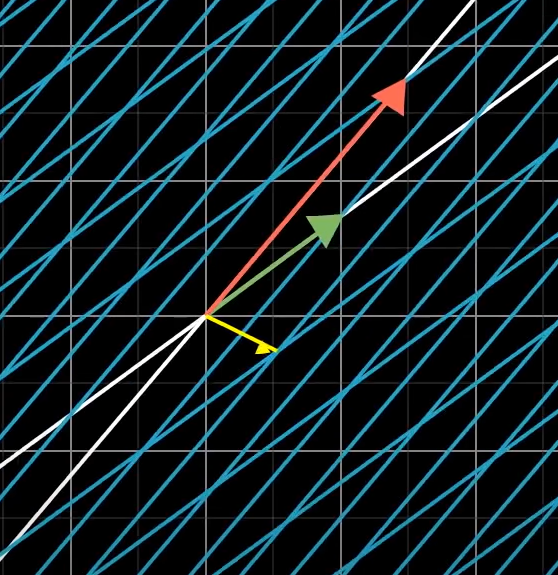
현재 살펴보고 있는 예제로 대입해보면, 람다를 변화시키며 det가 0인 값을 찾을 수 있다.

람다가 1일때, 선형변환으로 차원을 축소시킨다.
만약 아래와 같이 eigenvalue를 2라고 계산했을 때, eigenvactor를 찾으려면,

선형변환했을 때, 영벡터가 되는 벡터를 찾으면 된다. 계산해보면 (-1,1)을 지나는 span이 모두 그 값이다. 이는 변형하지 않은 원래 선형변환에서 이와 같은 span위의 모든 벡터가 2만큼 길이가 scaling 되고 위치는 변하지 않는다는 것을 의미한다.
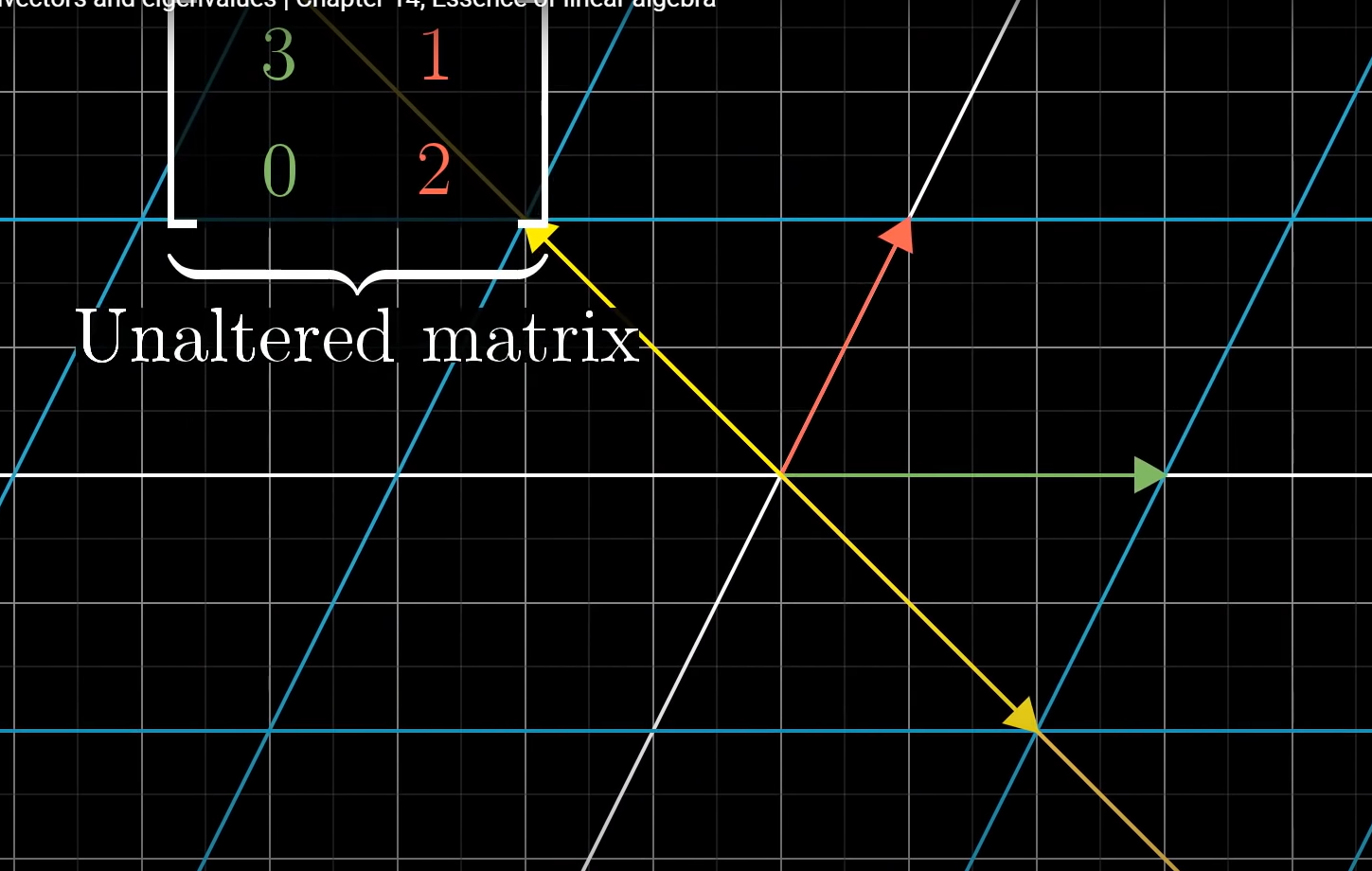
모든 선형변환이 eigenvector를 갖는 것은 아니다. 예를들면 회전 변환은 어떠한 eigenvector도 없다.
만약, 두 개의 basis vector가 우연히, eigenvector이면 어떨까?
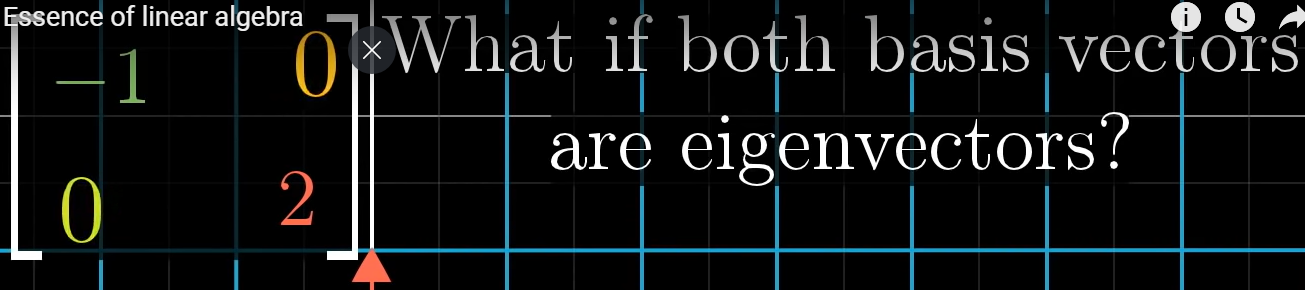
대각성분을 제외, 모든 성분이 0인 특징을 갖고 있다. 더 높은 차원도 마찬가지이다.

그리고 모든 대각 성분은 해당 eigenvector의 eigenvalue이다.
eigenvector가 basis이면 계산이 편리하다. 그래서 선형변환으로 eigenvector를 만들 수 있으면 변환 후 basis로 잡으면 편리하다. 이전 강의에서 basis 변환에 대해 설명한 것 참조하자.
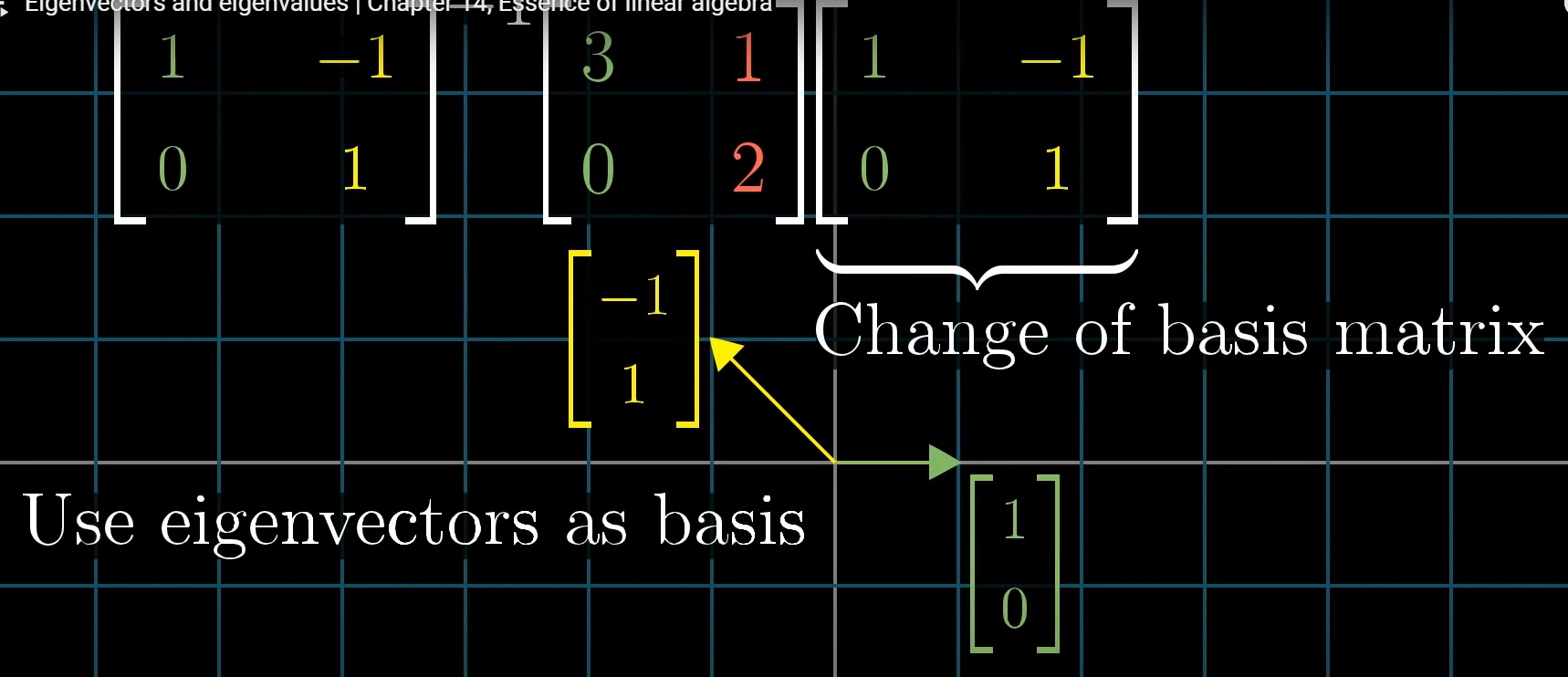
이는 같은 선형변환을 다른 basis vector로 표현한 것과 같다.
이렇게 계산한 선형변환 matrix는 대각성분이외에 모든 값이 0임을 보장한다.
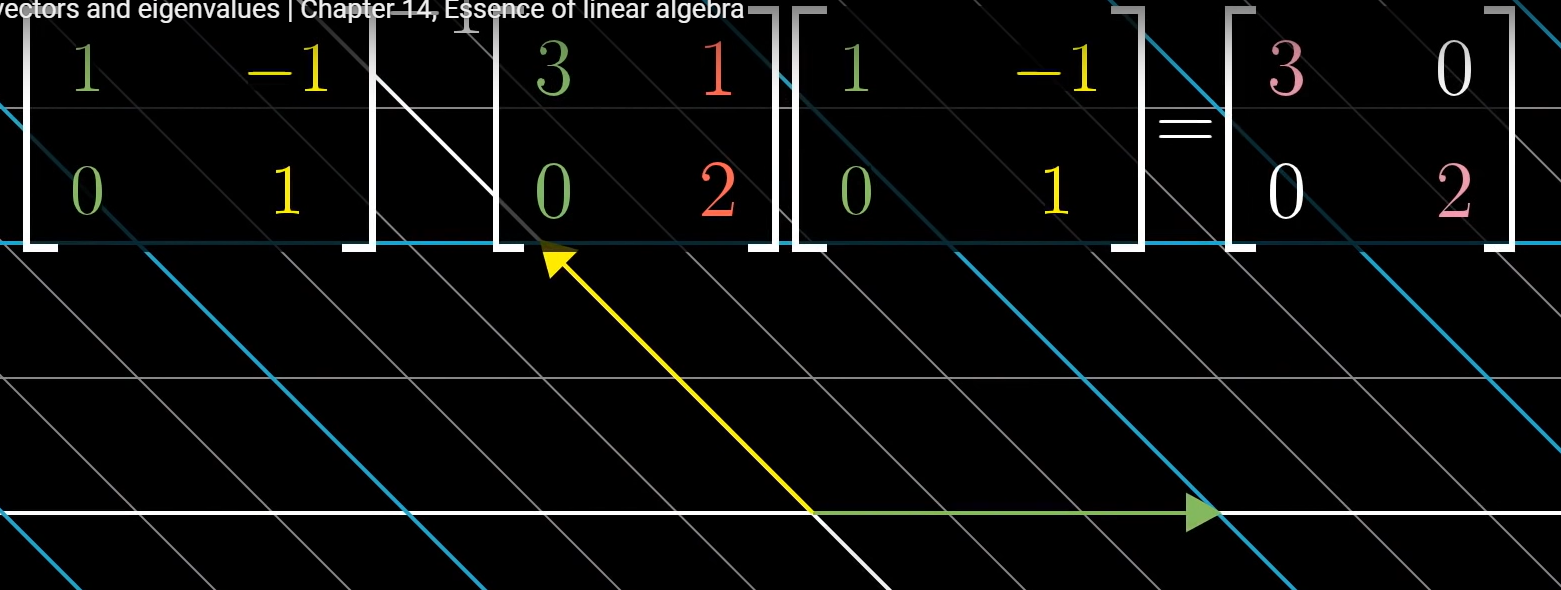
이는 eigenvector basis 관점에서 선형변환이 단지 scaling 한 것일 뿐이라는 것을 다시 한 번 알 수 있게 해준다.
eigenvector로 구성한 basis를 eigenbasis라고 한다.

위와 같은 matrix 계산한다고 했을 때, eigenbasis로 바꾼다면 계산이 매우 쉬워진다. 계산 후 다시 원래 시스템으로 바꾸는 작업을 해야한다.
참조 : (1) Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra - YouTube
'똑똑한 개발 > 수학' 카테고리의 다른 글
| Abstract vector spaces (0) | 2022.05.28 |
|---|---|
| A quick trick for computing eigenvalues (0) | 2022.05.26 |
| Change of basis (0) | 2022.05.14 |
| 크래머 공식을 기하학적으로 이해해 보자 (0) | 2022.05.11 |
| Cross product (ver.선형변환) (0) | 2022.04.23 |





댓글 영역