Cross product (ver.선형변환)

cross product 계산할 때 다음처럼 할 수 있다.

2번째 열에 벡터 v, 3번째 열에 벡터 w를 놓고 첫 번째 열에 기저벡터 기호를 넣은 다음 determinant를 구한다.

 

어떻게 가능한지 알아보기 위한 계획은 다음과 같다.

1. 벡터 v와 벡터 w로 표현한 3d to 1d 선형변환을 한다.

2. 1.의 dual vector를 찾는다.

3. 2는 벡터 v와 벡터 w의 cross product이다.

 

먼저, 두 개의 벡터를 행렬에 넣고 고정된 값으로 생각하고 첫 열을 variable로 생각해보자.

위 식은 3차원에서 수선으로 가는 어떤 함수이다.

 

 

위 식 세 개의 벡터로 이루어진 행렬의 부피를 구해보자.

벡터 v와 벡터 w로 이루어진 평행사변형의 넓이에 x,y,z로 이뤄진 벡터를 곱하지 않고 대신, 평행 사변형에 수직인 선에 [x,y,z]를 투영한 길이만큼 곱하여 구할 수 있다. 이는, [x,y,z]와 v w에 수직이면서 길이는 평행사변형 면적인 벡터와 dot product를 구하는 것과 같다.

 

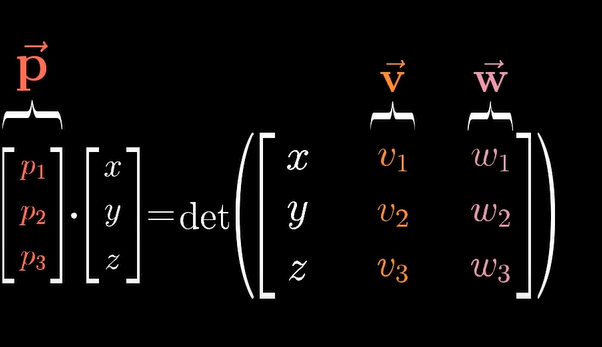
어떤 벡터 p와 [x,y,z]의 dot product를 구하는 것은 [x,y,,z]와 v,w 를 열로 가지는 3x3의 determinant를 구하는 것과 같다.

 

참조 : (2) Cross products in the light of linear transformations | Chapter 11, Essence of linear algebra - YouTube