고정 헤더 영역
상세 컨텐츠
본문
Dot product는 같은 차원 두 개의 벡터를 곱하고 더하면 구할 수 있다.

이를 선형변환과 연결시켜 생각해 볼 수 있다.

먼저 벡터 v에 벡터 w를 투영한다.
두 벡터의 dot product는 투영한 벡터 w의 길이 * 벡터 v의 길이이다.
두 벡터가 같은 방향을 가리키면 dot product는 양수가 되고
반대 방향을 가리키면 음수가 된다.
두 벡터가 직각이면 dot product는 0이 된다.



두 벡터의 순서를 바꿔도 dot product 결과는 같다.

dot product와 projection은 무슨 관계일까?
먼저 2차원의 벡터를 1차원으로 만드는 선형변환에 대해 살펴보자.
기저벡터의 도착지가 행렬이 열인 점을 이용해 선형변환 행렬을 만들 수 있다.


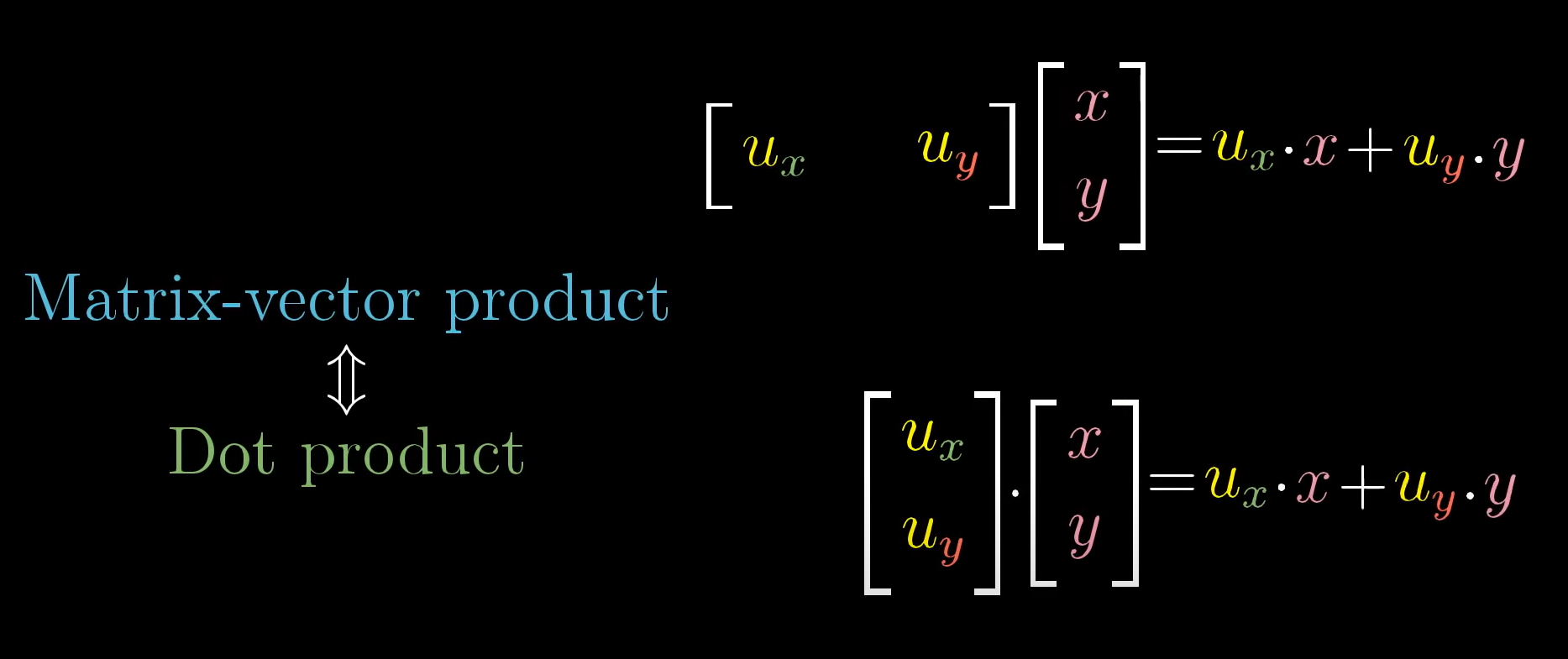
1x2 행렬과 2d vector에는 어떤 연관성이 있다.
입력이 2d vector이고 출력이 숫자인 선형변환과 벡터 자신과의 관계이다.
2차원 공간에 원점을 지나는 대각선 수선을 긋고 이 수선의 단위 길이에 해당하는 2차원 공간 벡터 u hat을 정의하면 아래와 같다.

2차원 공간점을 이 수선에 투영하는 모든 변환은 선형변환이다.
u hat과 i hat 모두 단위 벡터이기 때문에 u hat에 투영한 i hat은 u x좌표가 된다.
마찬가지로 u hat에 투영한 j hat은 u y좌표가 된다.

따라서 투영 변환을 나타내는 1x2 행렬은 u hat의 좌표가 된다.
[ux, uy]
위와 같은 이유로 단위 벡터와 dot product는 벡터의 투영 변환 후 길이와 같다.
단위 벡터가 아닌 dot product는 먼저 벡터에 투영한 길이에 벡터의 길이(단위 벡터의 몇 배)를 곱한 것과 같다.
2d to 1d linear transformation은 항상 2d의 어떤 벡터와 관련있다.
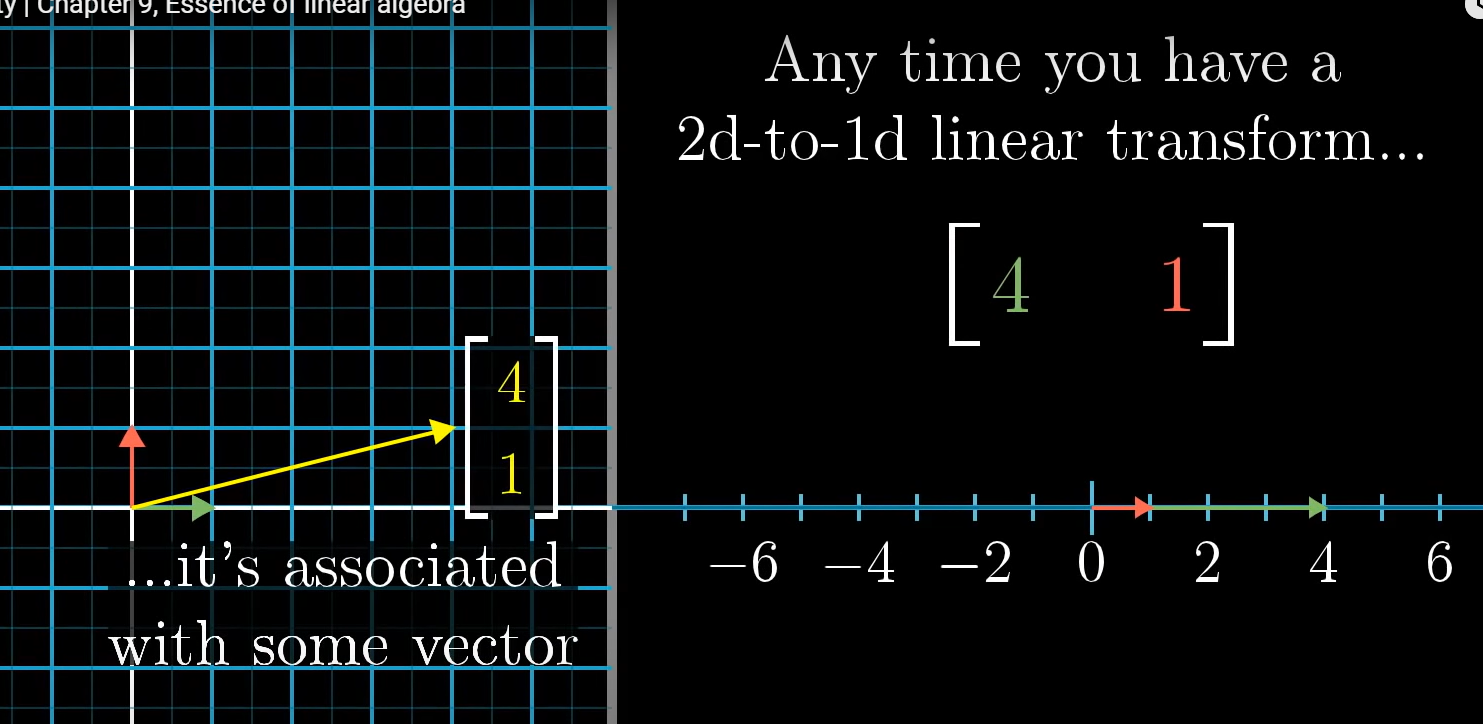
dot product는 투영에 관해 기하학적으로 생각해 볼 수 있는 좋은 툴이다.
참조 : (2) Dot products and duality | Chapter 9, Essence of linear algebra - YouTube
'똑똑한 개발 > 수학' 카테고리의 다른 글
| Cross product (ver.선형변환) (0) | 2022.04.23 |
|---|---|
| Cross product (0) | 2022.04.23 |
| Inverse matrices, column space and null space (0) | 2022.04.13 |
| Three-dimensional linear transformations (0) | 2022.04.10 |
| Matrix multiplication as composition (0) | 2022.04.09 |





댓글 영역